Overview
Although estimation is often a good strategy on both ISEE math sections, at times you will also need to do actual calculations to solve problems. Calculators are not allowed; students may (and probably should) write in the test booklet. If you’re taking the test online, make sure you have scratch paper to work on.
Know that there may be math on this exam that you have not yet learned in school. If you don’t understand a question, pick an answer and move on. If you partially understand a question, don’t get stuck; make a note and come back to it if you have time. Otherwise, in the last few minutes of the section, fill in an answer for every unanswered question.
Read carefully
One of the most common mistakes on the ISEE is misreading a question, usually due to reading too quickly. Be sure to take a few extra seconds on every question to avoid careless errors.
Underline important information.
This includes words and numbers indicating the quantities, relationships, and calculations (less than, twice, product, etc.) that you’ll need to answer the question. Words like “not” can be easily missed and completely change what youʼre supposed to find in the question!
Here’s an example of underlining:

Check that you answered the given question.
For every problem, after you finish solving, look back at what the question was asking you to find. Make sure that this matches your answer.
Here’s an example of this check:

It would be easy to accidentally solve for the number of miles Carla drove, which will almost certainly be one of the answer choices as a common error. Take the extra second to verify that the question is asking for Teresa’s miles, and answer accordingly.
Work backwards
For some questions, the jumping off point is in the answers. Take advantage of the fact that the ISEE gives you more information than just a question: it also gives you answer choices, one of which you know must be the correct answer!
For questions with an unknown quantity, you can substitute the answer choices for the unknown quantity to see which is correct. Always start with the middle answer choice to minimize the number of answers you have to substitute.

This is a tricky question to solve directly, but substituting answer choices is very manageable. Remember to start with one of the middle answer choices. Let’s try C: 9.
If there are 9 chickens, then there must be 8 pigs. The total number of feet will be 9・2 + 8・4 = 18 + 32 = 50. This is too few feet, so C is incorrect. To increase the number of feet, we must have fewer chickens and more pigs, so D must also be incorrect and we should try B: 8 next.
If there are 8 chickens, then there must be 9 pigs. The total number of feet will be 8・2 + 9・4 = 16 + 36 = 52.
B is the correct answer.
Estimate
Estimation is a powerful tool for eliminating wrong answers. For every question, before beginning to solve, ballpark what you think the right answer should be. Think about things like: should it be positive or negative, an integer or a fraction, bigger or smaller than any of the other numbers in the question, and so on. Sometimes the question will even include clues that you should estimate, such as “approximately” or “about,” but even without these words, always estimate first.
Here is an example of how to use estimation:

Notice that the question is asking how long it will take to read the REST of the chapter. Since almost the entire chapter has been read already, it cannot possibly take more than an hour to read the remainder, so you can immediately eliminate answer choices C and D.
Thus, even with very little time spent on this question, you have a 50% chance of answering correctly.
Pick values
Sometimes, the math questions you see on the Quantitative Reasoning and Math Achievement sections may seem very challenging to solve abstractly. The question may ask how an unknown quantity will change if it undergoes a couple of percent changes, or to solve for one variable in terms of others. In cases like these, it can be helpful to use actual numbers to determine the answer, rather than trying to solve algebraically.
Here is an example of how to use this strategy:
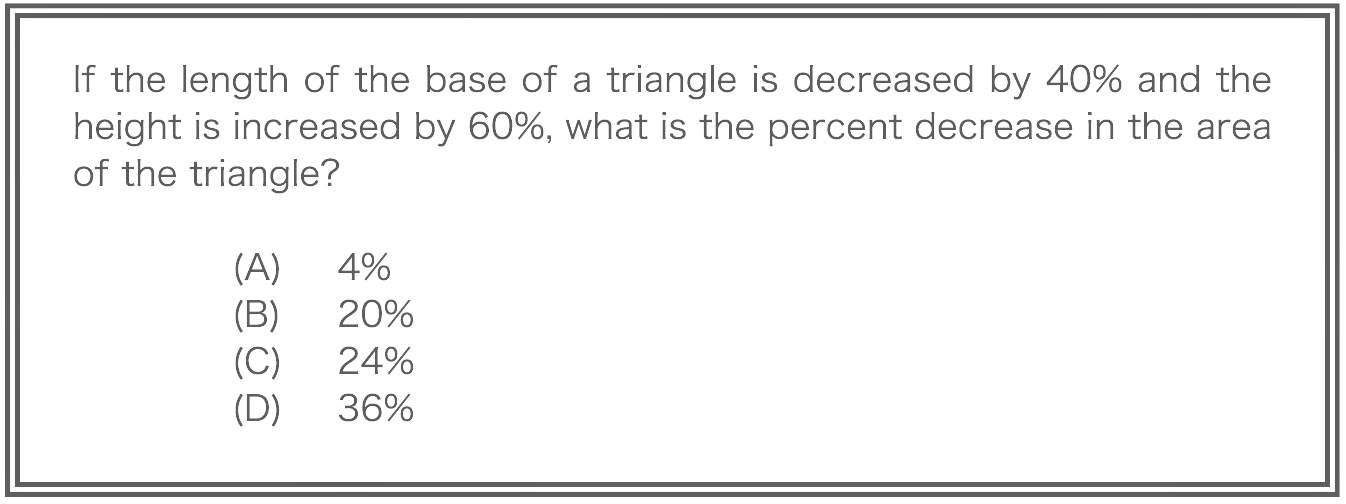
Pick easy values for the base and height of the triangle, say 10 and 20. Thus the initial area of the triangle is 0.5・10・20=100. (We chose these numbers strategically so that the area would be 100.)
Now the base decreases 40%, so the new base is 6, and the height increases 60%, so the new height is 32. Thus the new area of the triangle is 0.5・6・32=96.
Therefore, the area of the triangle has decreased 4%.
Tip: For percent questions, use 10% as your guide. 10% of any number is that number divided by 10, which is the same as moving the decimal point one unit to the left. Thus 10% of 60 is 6, 10% of 72 is 7.2, and so on.